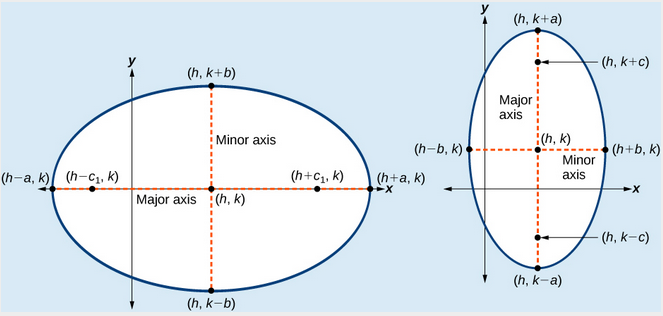
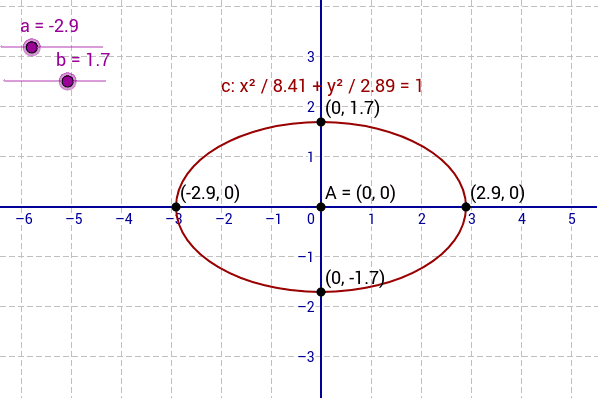
To graph ellipses centered at the origin we use the standard form a2x2 b2y2 1 a b for horizontal ellipses and b2x2 a2y2 1 a b for vertical ellipses. The center of this ellipse is the origin since 0 0 is the midpoint of the major axis.
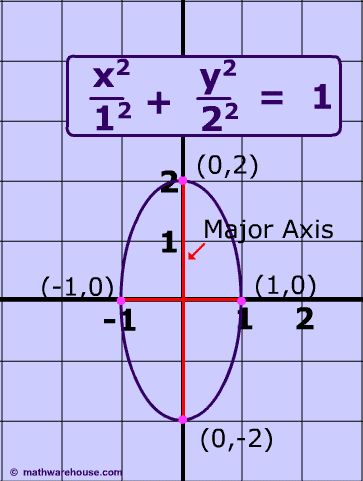
The major axis of this ellipse is vertical and is the red segment from 2 0 to 2 0.
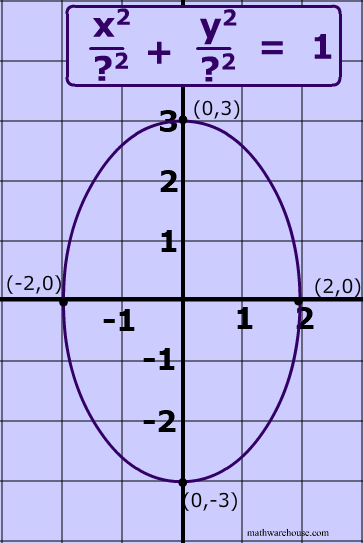
How to graph an ellipse from an equation.
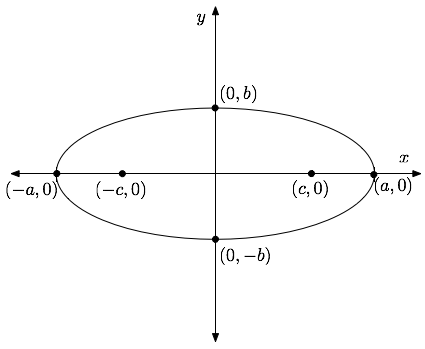
A is the distance from the center to either of the vertices which is 5 over here.
X 2 cy 2 dx ey f 0.
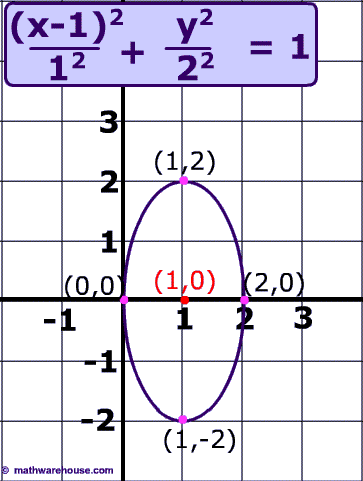
The equation is x h squareda squared plus y k squareda squared equals 1.
Ellipse standard equation from graph.
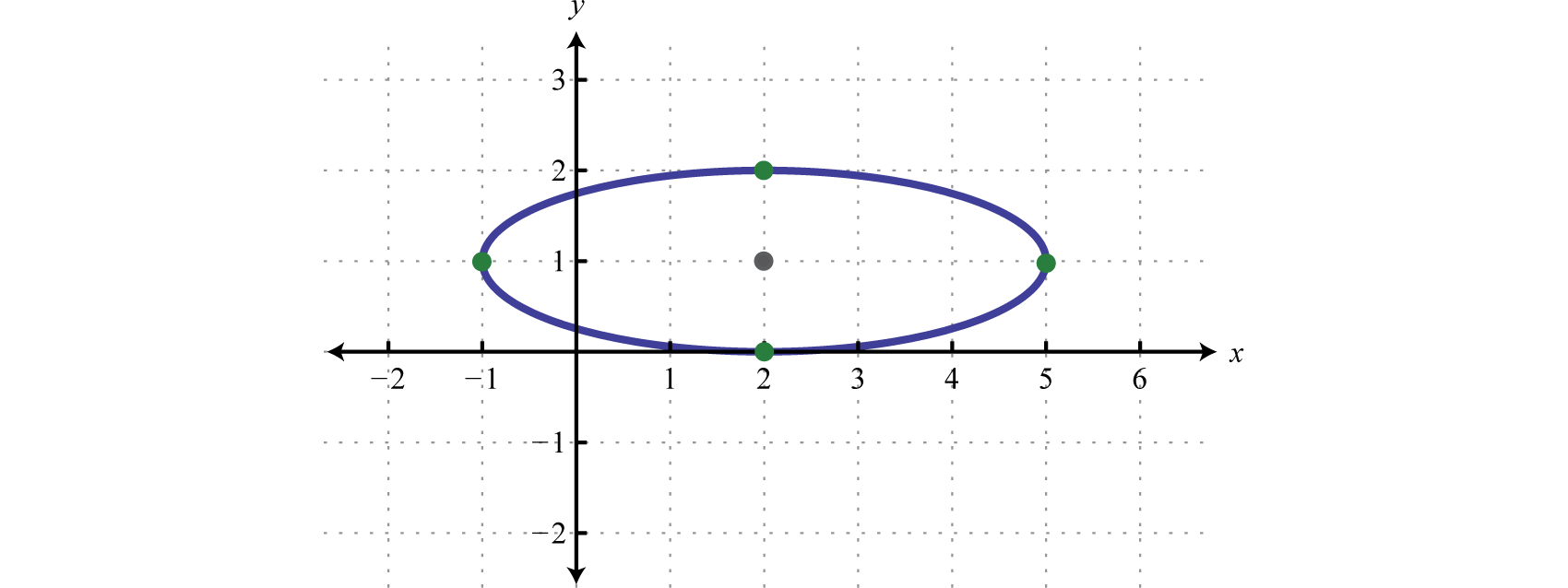
Use general equation form when four 4 points along the ellipse are known.
This is the currently selected item.
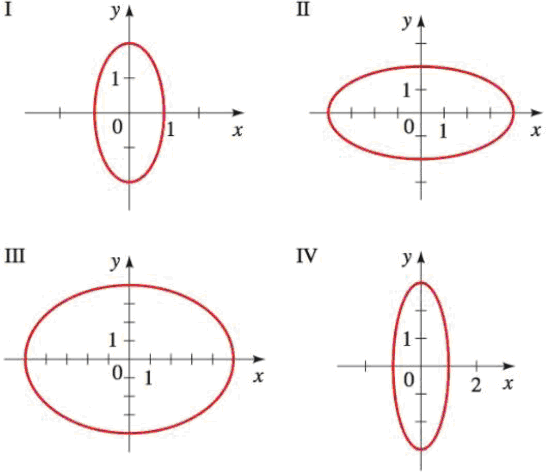
Graph features of ellipses.
Just as we can write the equation for an ellipse given its graph we can graph an ellipse given its equation.
B is the distance from the center to the top or bottom of the ellipse which is 3.
Add the constant to the other side.
Balance the equation by adding the new terms to the other side.
Ellipse standard equation from graph.
You then use these values to find out x and y.
Ax 2 cy 2 dx ey f 0.
In other words note.
To solve for an ellipse either one of the following conditions must be known.
How to graph an ellipse.
The general equation of an ellipse is either of the following forms.
Center radii of ellipses from equation.
Center and radii of an ellipse.
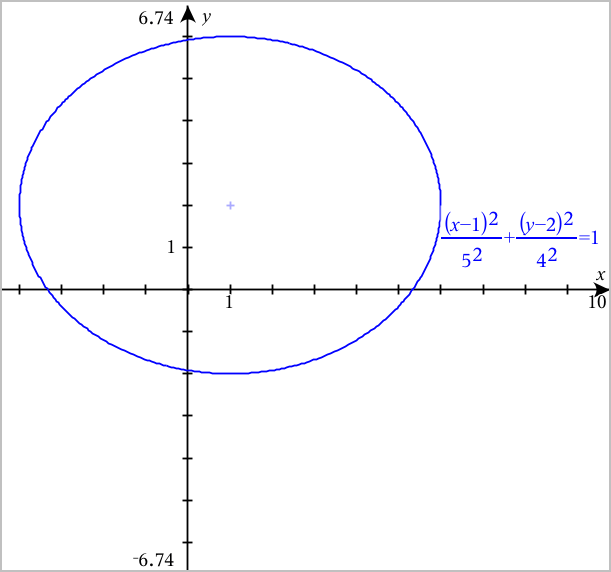
Example of the graph and equation of an ellipse on the.
Well the equation of the ellipse is going to be x minus the x coordinate for the center squared over here over the horizontal axis is horizontal radius squared plus y minus the y coordinate of the center squared over the vertical radius squared.
You need to factor out two different constants now the different coefficients for.
General equation of an ellipse.
The value of a 2 and b 1.
The general equation of an ellipse is where a c but have the same sign.
Adding 1 and 4 inside the.








No comments:
Post a Comment